A theorem of Bulatov, Jeavons and Krokhin states that when the algebra associated with a core template does not lie in a Taylor variety, then the CSP for that template is NP-complete. In the same paper, the authors conjecture that in all other cases, the corresponding CSP is solvable in polynomial time. Maroti and McKenzie showed that an algebra generates a Taylor variety if and only if it has a $k$-ary weak near-unanimity (WNU) operation for some $k$; this shifts the search for a proof of the algebraic dichotomy conjecture to focus on WNU operations.
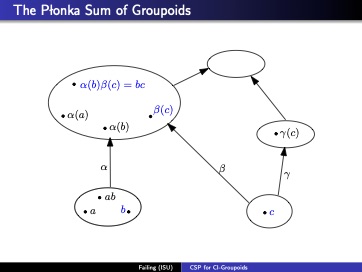
A binary operation is a WNU precisely if it is commutative and idempotent, and a semilattice operation is known to be sufficient for the tractability of an algebra. Using Prover9 and the Universal Algebra Calculator, we investigate several weakenings of associativity and show that they too are sufficient for the tractability of a finite commutative, idempotent groupoid. In particular a finite CI-groupoid has a tractable CSP if it satisfies any of the following identities: $x(y(xz)) \approx x((yx)z)$, $x(y(yz)) \approx ((xy)y)z$, $x(yz) \approx (xy)(xz)$. A key tool is the theory of Plonka sums. Roughly speaking, we prove that a finite Plonka sum of finite algebras lying in a tractable variety is tractable.